Страшная сказка про три цветных квадрата...
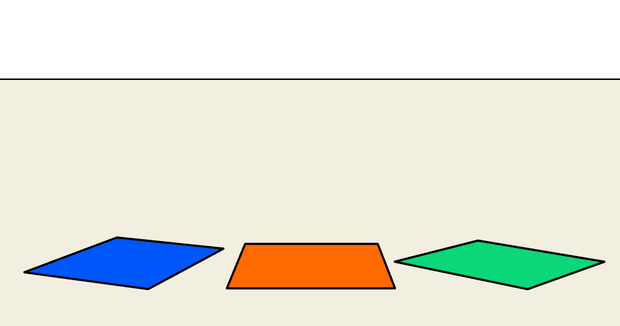
Для тех, кто хочет вспомнить основы "перспективы"… Жили-были на одной плоскости три цветных квадрата.…И один из них – был лишним! Определите, какой именно…
Собственно, на этом задача кончается и лучше дальше не читайте, а сразу принимайтесь за решение… Потому что дальше начинается самое страшное! Дело в том, что петляя по тропинкам дремучего леса под названием “Перспектива”, мы еще ни разу не приближались к логову страшного зверя под названием:”Точка зрения”! Эта страшная зверюга пожирает всех подряд – и опытных и начинающих! Но особенно опасна она для начинающих! Юные дарования, когда берут в руки карандаши-краски и смотрят на чистый белый лист бумаги, даже не подозревают, какое страшное чудовище обитает в глубинах этого листа. И стоит им только попытаться изобразить, не что-то “плоское”, а пойти “вглубь”, то это чудовище выныривает из бездны и…
А бывает так. Опытный мастер заканчивает эпохальное полотно и идет спать, решив, что завтра утром он двумя-тремя точными мазками завершит этот шедевр, достойный его гения! И не знает он, что коварная Точка зрения уже давно за ним наблюдает! И когда наш мастер на следующий день подходит к своему бессмертному творению, то свежим глазом он видит, что все пропало! Все выглядит неестественно вывернуто, линии клонятся куда-то вбок, да и вообще все кривое! В истерическом порыве рвет свой шедевр в клочки наш художник и идет за бутылкой!
А, еще бывает... Нет!... Слишком страшно, не будем рассказывать! Заметим только, что, например, в некоторых, особо тяжелых случаях, небольшая скромная комната - превращается в тоннель метро!
Точку эту коварную никто никогда не видел, но, говорят, что можно иногда увидеть ее отражение на линии горизонта... Так вот, все квадраты (и даже круги), лежащие во всех плоскостях, подчиняются этой злодейке! А тут недавно вышла одна сильно научная книга, где утверждается, что бывает и две и четыре и даже больше точек зрения! С одной бы точкой справиться, а уж с несколькими…
В течение столетий много художников сгинуло, пытаясь ее найти и победить!
Попробуйте и вы! (Хотя, на вашем месте – я бы не стал рисковать!)
Да, для тех, кто сказку не читал, или вообще ничего не понял: цвет квадратов – роли не играет…
Идею этой задачи подсказал Лев Степаненко ( https://illustrators.ru/users/id7235 ), за что ему - персональное спасибо!
А сказочка дурацкая – это моя (он – не виноват!)…
такое ощущение,что они все в разных плоскостях:)
Согласен.
Э-э...- нет, по условиям задачи, - они находятся в одной плоскости. Можно считать, что она - горизонтальная, хотя под эти условия подходят и другие. Страшная сказка об этом и говорит, что все что мы рисуем, как будто будет на своих местах, а на самом деле - криво!
Лень чертить, но и так видно - синий )
Честно говоря, я специально подбирал простой вариант, в котором можно просто угадать (хотя здесь - главное, конечно не угадать, а понять в чем суть.) Нет, не синий!
Я ставлю на желтый.)
))) Тихо!!! Только я и Вы видим желтый, не палите контору )))
Малевич бы на чёрный поставил:)
Ставка, принимается, но мы же не в цветные стеклышки играемся: суду нужны веские доказательства!
Даа, всё оказалось сложнее, чем я мог предположить.
Это да! Пришлось несколько расширить трактовку, так как мы можем столкнуться с разными квадратами, а не только с "фронтальными"! Будем подводить общую "базу" под все решения...
отличная тема
Спасибо! Просто, пока критики не подтянулись...
Кстати, можно в сказочку еще добавить, что "Точка зрения" - питается не только художниками, она не брезгует и фотографами! Сделает один такой фотографию красивой площади, глядь: "Что это?! Ничего не узнать!..." Вся площадь вытянулась в глубину, исказилась до неузнаваемости! Не приходилось с подобным сталкиваться?
Итак... Представим, что вырезали мы из бумаги эти самые квадраты, положили их перед собой на стол, сделали пару шагов назад и зарисовали (или сфотографировали). Затем отошли еще немного и опять зарисовали-сфотографировали их уже с новой точки.
Затем, чтобы зло подшутить над коллегами художниками, один квадрат из первого изображения - заменили квадратом из второго! (Пусть поломают голову!). Вот... можно думать дальше...
Случаем не зелененький? У него вроде линия горизонта ниже... Проверила бы, но комп включать лень.
Лень - великий двигатель прогресса! Но так мы злодейскую точку - не одолеем: она - хитра и коварна! В конце концов, покусает она нас всех и придется по сорок уколов делать! А с горизонтом - нет, они все аккуратно располагаются на одной плоскости, все сходится на горизонте, как и положено...
может синий? Подозрительно он выше остальных))
Мысль - интересная! Но никто не говорил, что квадраты - одинакового размера...
Немного отвлекаясь: была, в свое время, небольшая чудесная книжечка, где были подробно раскрыты некоторые сложные моменты (в том числе и этот). Если кому встретится, - очень рекомендую!
если они все квадраты и все в одной плоскости, а цвет не в счёт, то по какому принципу вы хотите выбрать лишний?
Ну, цвет, - это только чтобы веселее было (сказка - очень уж страшная!). А вот принцип, по которому один из них "лишний" - это и есть "гвоздь программы". Хотя, в принципе, мы уже его немного приоткрыли (см. комментарий выше)... Осталось только применить легкие построения, чтобы его "ущучить"...
Сходила в комп. Почертила. Рыжий выходит. У него h до линии горизонта меньше чем у остальных. Хотя мож я неправильно искала:)
Хорошо бы чертежик (его можно приклеить в режиме "корректировки комментария"). Любопытно, хотя и неправильно...
Кстати, эта тема должна быть особенно интересна тем, кто использует в своих работах фотографии (например военной техники, или зданий). Их "вписывание" в картину - это почти то же самое, чем мы занимаемся...
Так...самое время подбросить небольшой путеводный клубочек: для этого просто вспомним как определяются углы (в первую очередь - прямые)... Это, например, для зеленого квадрата.
разве в условии задачи не жестко сказано, что все они квадраты?
зачем нам измерять их прямые углы?
А, вот так выглядит та же операция с красным (пожалуй, в самом деле "оранжевый"):... Видите, в чем разница?! Остается только выяснить: к какой "системе" принадлежит оставшийся "синий"...
Круто:)
Альтернативный поворот выдам)))
Если все три прямоугольника "надстроить", условно, в "равносторонние" параллелепипеды, то с моей "точки зрения", на изображение "куба" в пространстве претендуют две левых фигуры. И какая теперь лишняя?)
Павел, направление - интересное, вот - достроил квадраты до кубов...
у зелёного точки схода не лежат на линии горизонта
Нет - нет, это просто издержки небольшого масштаба и короткой базы на которой строится отрезок (обычная проблема для перспективы). Антон (всегда восхищаюсь Вашими городскими зарисовками!), представьте: Вы рисуете площадь, на ней - квадратный фонтан... В зависимости от того, находитесь Вы ближе, или дальше этот квадрат - получается различным! При этом все - на месте и линия горизонта и все что положено - на ней сходится... Собственно, мы и выясняем, как "поймать" и зафиксировать эту самую точку зрения на уже готовом изображении...
Кстати, определив точки схода для "синего" квадрата - Вы почти решили задачу, т. к. остается сделать один завершающий шаг...
Зря вы про критиков.Как раз таки это нормальная тема.
Я вижу что не в компании....оранжевый.
Не читал прав не прав
Илья, я рад, что Вы к нам присоединились! Нет, не оранжевый! Мы ведь уже выяснили, что все они - правильные квадраты, лежат на одной плоскости, цвет, угол поворота и т. д. - все это не важно! Важно другое: они нарисованы с разных точек! Выглядит это примерно так:
Пока наша бессмысленная задача про три квадрата не "засохла" окончательно и не ушла в историю, хотелось бы показать, как это применяется на практике... Итак. Мы сделали набросок интерьера (может быть сарай, или бассейн - главное, чтобы угол был прямым), и определяем линию горизонта и точки схода. До сих пор - все понятно и обычно. Но, вдруг, нам, зачем-то понадобилось нарисовать на полу... коврик, причем он лежит под произвольным углом к стенам (это может быть стол, стул и т. д.) Вот здесь нам и понадобится та самая страшная "Точка зрения". Другими словами, нам нужно определить ту самую точку, с которой мы все это рисуем! Сделать это можно следующим образом: (см. изображение). Если же мы этого не сделаем, нам останется, только "ловить на глаз" - и не факт, что поймаем...
Интересно...А то, что вершины прямых углов во фронтальной плоскости ( ну да, вроде фронтальной...) сощлись в одну точку, это система? Или частный случай?
это конечно очень полезно,не спорю. Помню случай ,рассказывали друзья,парень нарисовал натюрморт,и на стене был типа календарика листок.И вот краска по цвету и прозрачности так удалась...что была полная иллюзия что это реально приклееный к картине листок бумаги.К чему я.....специалист по мозгу Савельев ,утверждает , что все мы видим по разному. И вот как бы там не сходились линии,как бы ни был правильным чертёж..я вижу ,хоть убей именно оранжевый квадрат.Будь он и правильно уложеннымИ написал именно на то....как мне видится.Я не проверял линии и черетежи
Ага, сработала ловушка! Оптические иллюзии в перспективе - отдельная и очень интересная тема! Ну, раз уж все наши секреты раскрыты, - то "карты на стол"! Вот так выглядели бы эти квадраты, нарисованные все с одной точки (общей для оранжевого и синего)...
Что до глубин мозга... Не-ет, у нас задачи гораздо скромнее - мы исследуем вопрос: "как использовать геометрию для нужд народного хозяйства!" А тонкости психологии, типа: "один на картинке видит розу, а другой - страшное чудовище", - это не для нас...
Илья, и Дмитрий.
Вот, перед вами стоит натюрморт.
Если, поочередно смотреть на него левым, и правым глазом? Какую точку обозрения вы выберете?
Это - сложная задача! Но, только в том случае, если натюрморт состоит из одного спичечного коробка, подвешенного перед самым носом...
я всё опять - с практической стороны вопроса:
ну, хорошо, когда карты, раскиданные на столе, или колёса автомобильчика - всё имеет 4 точки на какой то плоскости - это всё как то ещё можно расчертить...
а вот как решать задачи, когда в готовый пейзаж - нужно вписывать недостающие там элементы архитектуры и какие либо прочие предметы, где этих 4х точек нет-? ... т.к. формы сложные, но любое отклонение от нужного ракурса - тут же вызывает сомнение, что в композИшке чав0йто не так...
а тридЭшничок ради одного случайного заказа - осваивать - нет резону.
с таким - рано или поздно, кАжный практикующий 2дэ маляр - сталкивается... и не раз...
тут бы можно было найти непаханое поле для задачек
* ͜ *
С этим все просто - в любом приличном учебнике по "перспективе" (например: А. Г. Климухин, "Начертательная геометрия" ) есть раздел: "Реконструкция изображения". И в этом разделе перечислены условия, при которых такая реконструкция может быть выполнена. Так что, если перед нами картина "Поле до горизонта", то - мы мало что с ним можем сделать (не за что зацепиться!). И 3D - не очень поможет (им, правда легче подгонять фигуры, просто "сплющивая" изображение)...