Кино…и немцы…С праздником!
Для тех, кто хочет вспомнить основы "перспективы". Кино, правда, какое-то невпечатляющее (современное, надо полагать). И с серьезным “киноляпом”! Впрочем, обо всем – по порядку...
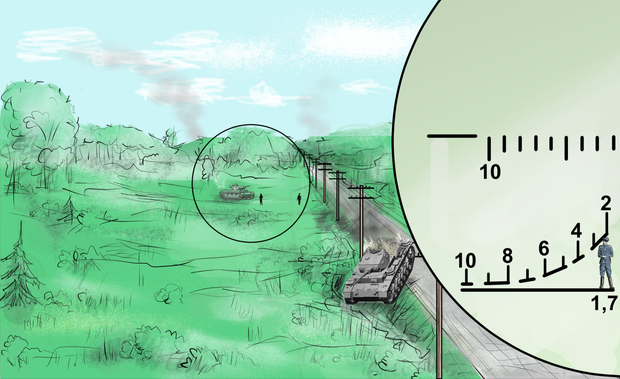
Сюжет: немцы безуспешно пытаются прорваться вдоль шоссе, собирают силы для очередной атаки. Наши – на небольшом возвышении рядом с дорогой (можете сразу прикинуть на какой высоте). Снайпер с помощью оптического прицела старается определить точное расстояние до немецкого офицера (по специальной шкале). И…вот она главная халтура: такие прицелы появились только после войны!
Внимание, вопрос: какое это все отношение может иметь к художникам-иллюстраторам?!
Однако, не спешите.… Несколько поколений художников училось по известному учебнику А. П. Барышникова “Перспектива”. Он выдержал несколько изданий и популярен до сих пор.
Так вот, автор учебника уделил этому вопросу целый раздел, он особенно подчеркивал важность изучения закономерности изменения высоты фигур (и вообще размеров предметов), в зависимости от глубины пространства.
Прицелов в той книге, конечно не было, но просто нам особенно повезло изучить проблему на конкретном материале.
Итак, вопрос: почему шкала для определения расстояния имеет криволинейную планку, ведь мы все привыкли, что все высоты “убывают” в глубину линейно, например, мы можем это наблюдать по ряду телеграфных столбов…
(Да, для тех, кто не "не в теме": шкала подводится к фигуре человека и по той риске под которую он “влезет” и определяется расстояние в сотнях метров).
Любопытно, что несколько лет назад в Интернете развернулась бурная дискуссия по данному вопросу: http://forum.guns.ru/forummessage/2/1608939.html
Впечатляет, чья-то реплика:”Какой-то крышеснос!”. Ну, это они погорячились, вопрос не такой уж и сложный!
Ответ – лежит на поверхности…
Кстати, для особенно въедливых: можно ведь прикинуть расстояние еще и по телеграфным столбам (между ними – 50м). А тогда, - расстояния не совпадут!
Опять нас пытаются обмануть…
Так запутанно... "по той риске под которую он “влезет” и определяется расстояние в сотнях метров". Так на одном и том же расстоянии может стоять человек и 150 см и 190. Откуда мы знаем какого роста человек влезший по риску?
1,7 (под шкалой) - это усредненная высота человека. Мы можем "привязаться" только к известным нам размерам, высота человека - более-менее годится...
Дмитрий, с праздником!
Судя по столбам, до них метров 200-250, если я правильно поняла. А вот по шкале непонятно. Может шкала имеет криволинейную планку потому что прицел это круг? Может эту шкалу как-то накладывают на круг и измеряют расстояние?
Наверное глупое предположение, но других пока нет))
Ольга, спасибо! Нет, прицел, это круг, конечно, но для иллюстраторов вся эта "прицельная" экзотика вряд ли интересна, другое дело, что за всем этим скрывается таинственный геометрический закон...
Да, задача конечно необычная, "боевая", но не в смысле прицеливания, а просто надо посмотреть и прикинуть, как вообще на картине появляется изображение...
Это, наверное, потому что у нас зрачок круглый. Если бы он был у нас прямой палочкой, как у козы, тогда бы и планка была прямолинейная.
Для козы, определенно, прицел потребуется несколько видоизмененный...
Может до них 570 -580 м ?
Шкала деления измеряется в сотнях метров, например там где цифра 2 - это 200 метров, так?
Нет-нет, до них именно 200 метров (мы верим шкале прицела!). На самом деле, первая часть вопроса - довольно простая (чуть разобраться, только...).
Гораздо интереснее вторая часть: по прицелу - 200 м, по столбам - 150 м. Вопрос: куда делась часть дистанции?
В принципе, и первая и вторая части становятся очевидными, если мы просто карандашиком на клочке бумаги набросаем эскизик-схемку, как мы получаем изображение вообще (классически: глаз, картина, лучи зрения и т. д.)...
Ну, шкала по дуге - так нам нужно не расстояние определить, а угол подъема ствола винтовки. Так как пуля летит по дуге (закон тяготения никто не отменял), то и угол наклона меняется нелинейно. Думаю, причина в этом. Это не расстояния в метрах, а поправка на прицел.
Никоим образом! Нас как иллюстраторов не интересует, конечно, баллистика, законы тяготения, траектории, поправки прицела и т. п. Нас интересуют исключительно законы изображения!
Можно рассмотреть это дело так. Забудем про прицел и попробуем представить как изменяется наше представление о величине человека по мере его удаления (в кратных величинах, например по 100 метров). Еще проще просто нарисовать это в привычной форме (с помощью проекции на картину). Попробуйте, могу заверить, что результат вызывает сильное удивление!
Может потому что земля круглая :)
Про круглость земли, мы, может быть, сочиним со временем специальную загадку, а здесь все до банального просто!
Можно поступить следующим образом. На обычной картине нарисуем от левого ее угла пять столбов, на равном расстоянии в глубину картины (перпендикулярно к ней) и такие же столбы на таком же расстоянии но уже параллельно картине (точнее, - прямо на ней!).
Теперь высоты первой группы можно наложить соответственно на вторую и посмотреть, что же мы, в конце концов, получили...
Звучит запутанно, но сделать это можно быстрее, чем написать этот текст!
Тот, кто сумеет разгадать эту "криволинейную" загадку, тот, возможно, приблизится к раскрытию тайны пространства-времени и сделает возможными путешествия в далекий космос!
И, может быть, однажды, мы всей "иллюстраторской" компанией загрузимся в космический корабль и отправимся на "пленер", куда-нибудь в одну из галактик туманности Андромеды, рисовать местные пейзажи...
Было бы интересно глянуть на местные достопримечательности этой туманности )))
Занимаетесь какой-то софистикой если честно, сами себя только обманываете
Говорите перспектива у Вас линейная? -Ну да
А черточки неправильные мол под дугой? -Нет, они вполне верны
Ну а почему они верны? - у Вас же линейная перспектива - т.е. все построенные параллельные Вы изображаете в пространстве как сходящиеся. Т.е. вот изображены столбы. Построены они на основе двух сходящихся прямых, соединяющих верхние и низшие точки столбов. Обосновано это схождение якобы сокращением размеров с увеличением расстояния от зрителя. Все как по правилам схемы для изображения пространства.
А теперь Вы накладываете правила этой схемы на совершенно иную, где играют другие правила, а не законы "круглых глазиков"
Высота человечков задана под сокращением - т.е. если бы они были в пространстве - прямая, проходящая через их головы сокращалась бы к горизонту и сближалась бы к другой прямой, проходящей через ноги, и которая тоже бы сокращалась к горизонту!
Но! Это иная схема, повторюсь! В ней нижняя прямая показана без каких либо сокращений! Расстояния между человечками сохранены без изменений! Сделано это для более удобного ориентирования глазеющего в лупу (снайпера), где ему будет легче определять расстояние "плавающего" человечка, который ни 2 ни 4, а где-то между ними.
Т.е. если бы нижняя прямая с увеличением расстояния от зрителя сокращалась так же, как и верхняя прямая - то никакой дуги бы и не было.
Для подтверждения - просто нарисуйте в любом пеинте столбики сначала в перспективе, а потом эти столбики скопируйте и вставьте в ряд на одинаково удаленном друг от друга расстоянии.
Приятно читать такой подробный комментарий! Правда, не вполне соглашусь: Штирлиц, например, употреблял термин "софистика" как неуместное и излишнее философствование, а у нас - все предельно точно, конкретно и по делу!
Но в остальном, - примите поздравления: это именно то, что требовалось! Единственное, я бы подсократил Ваш текст, иначе кто-то, решивший плотно разобраться в сути проблемы натолкнется на "круглые глазики", "иная схема" и т. д.
Запутается человек, ведь это не разные "схемы", а одна проекция, где мы определяем размеры предметов, в зависимости от точек пространства...
А так, - все замечательно: задача - решена! Позволю еще от себя добавить парадоксальное следствие данного явления: при удалении предметов, их кажущаяся величина начиная с определенного расстояния будет меняться очень мало! Дальние предметы мы видим уже практически в параллельной проекции...
Может кому-то это и пригодится: шибко удаленные об'екты - это практически аксонометрия...
Ну, что же, побольше бы таких развернутых записок, веселее бы дело пошло! Кстати, почин - прекрасен, так давайте продолжим, там ведь есть еще продолжение банкета!..
Было бы интересно довести эту тему до конца...
Приветствую всех-!
* ͜ *
всё кино я ч0Тт пропустил :)
но глянуть, чево тут делается - было занимательно
.
про художнегов и оптические приборы - добавлю, пожалуй:
...
мне оно ни только интересно, но и по прямым проф. навыкам - полезно. т.к. без цифровушки нынче - никуда, то
средне обычный зумм можно использовать, ещё и как - точный прибор измерения расстояний (и размеров). если в кадре есть объект, который известен по своим габаритам, или, если сделать вот такие "пристрелочные кадры"
(смотрим 2 фотки ниже, которые я делал ещё для той задачки с размерами Луны), тогда можно лехко вычислить любые расстояния до предметов.
на 10 километров дистанции - точность выходит до полуметра, а если в кадре видно спичешный коробок размером на 4 пикселы, то на 70 метров дистанции - погрешность всево лишь - 3 сантиметра.
при габаритах самого кадра - 4608х3456 пиксел
* ͜ *
полезность, разумеется, в том, что (не особо напрягаясь)
всего за пол года можно натренировать свой глазомер до чудодейственных показателей.
а такая весч, как "глаз-алмаз" - для многих проф. навыков - штука бесценная...
ну, и рисовать начнёте, вааще, как б0хх
:)
такшта-а... совмещаем приятное с полезным, фотаем плироду, и совершенствуем вверенное нам при рождении
физ. оборудование
.
и - желаю успехов, кому (из юных и дерзких)
"оно"дошло до сознания
* ͜ *
И сколько там до этого объявления на кирпиче? Метров 100? А, если ещё увеличить, то можно и прочитать, что там написано?
Джентельмены, а немца уже пристрелили? (с)
Выстраивали теорию и про него как-то забыли в суматохе...